Part III

References

Memory Addressing, Binary , and Hexadecimal Review

You do not have to understand the concepts in this appendix to become well-versed in C++. You can master C++, however, only if you spend some time learning about the behind-the-scenes roles played by binary numbers. The material presented here is not difficult, but many programmers do not take the time to study it; hence, there are a handful of C++ masters who learn this material and understand how C++ works “under the hood,” and there are those who will never master the language as they could.

You should take the time to learn about addressing, binary numbers, and hexadecimal numbers. These fundamental principles are presented here for you to learn, and although a working knowl- edge of C++ is possible without knowing them, they greatly enhance your C++ skills (and your skills in every other programming lan- guage).

After reading this appendix, you will better understand why different C++ data types hold different ranges of numbers. You also will see the importance of being able to represent hexadecimal numbers in C++, and you will better understand C++ array and pointer addressing.

Computer Memor y

Each memory location inside your computer holds a single character called a byte. A byte is any character, whether it is a letter of the alphabet, a numeric digit, or a special character such as a period, question mark, or even a space (a blank character). If your computer contains 640K of memory, it can hold a total of approxi- mately 640,000 bytes of memory. This means that as soon as you fill your computer’s memory with 640K, there is no room for an addi- tional character unless you overwrite something.

Before describing the physical layout of your computer’s memory, it is best to take a detour and explain exactly what 640K means.

K means approxi- mately 1000 bytes

and exactly 1024 bytes.

Memory and Disk Measurement s

By appending the K (from the metric word kilo) to memory measurements, the manufacturers of computers do not have to attach as many zeros to the end of numbers for disk and memory storage. The K stands for approximately 1000 bytes. As you will see, almost everything inside your computer is based on a power of 2. Therefore, the K of computer memory measurements actually equals the power of 2 closest to 1000, which is 2 to the 10th power, or 1024. Because 1024 is very close to 1000, computer-users often think of K as meaning 1000, even though they know it only approximately equals 1000.

Think for a moment about what 640K exactly equals. Practi- cally speaking, 640K is about 640,000 bytes. To be exact, however, 640K equals 640 times 1024, or 655,360. This explains why the PC DOS command CHKDSK returns 655,360 as your total memory (assuming that you have 640K of RAM) rather than 640,000.

M means approximately 1,000,000 bytes and exactly 1,048,576 bytes.

Because extended memory and many disk drives can hold such a large amount of data, typically several million characters, there is an additional memory measurement shortcut called M, which stands for meg, or megabytes. The M is a shortcut for approximately one million bytes. Therefore, 20M is approximately 20,000,000 charac- ters, or bytes, of storage. As with K, the M literally stands for 1,048,576 because that is the closest power of 2 (2 to the 20th power) to one million.

How many bytes of storage is 60 megabytes? It is approxi- mately 60 million characters, or 62,914,560 characters to be exact.

Memory Addresse s

Each memory location in your computer, just as with each house in your town, has a unique address. A memory address is simply a sequential number, starting at 0, that labels each memory location. Figure A.1 shows how your computer memory addresses are numbered if you have 640K of RAM.

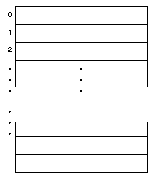
Figure A.1. Memory addresses for a 640K computer.

By using unique addresses, your computer can track memory. When the computer stores a result of a calculation in memory, it finds an empty address, or one matching the data area where the result is to go, and stores the result at that address.

Your C++ programs and data share computer memory with DOS. DOS must always reside in memory while you operate your computer. Otherwise, your programs would have no way to access disks, printers, the screen, or the keyboard. Figure A.2 shows computer memory being shared by DOS and a C++ program. The exact amount of memory taken by DOS and a C++ program is determined by the version of DOS you use, how many DOS extras (such as device drivers and buffers) your computer uses, and the size and needs of your C++ programs and data.

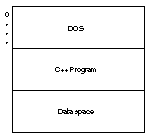
Figure A.2. DOS, your C++ program, and your program’s data share the same memory.

Bits and Byte s

You now know that a single address of memory might contain any character, called a byte. You know that your computer holds many bytes of information, but it does not store those characters in the same way that humans think of characters. For example, if you type a letter W on your keyboard while working in your C++ editor, you see the W on-screen, and you also know that the W is stored in a memory location at some unique address. Actually, your com- puter does not store the letter W; it stores electrical impulses that stand for the letter W.

The binary digits 1 and 0 (calledbits) represent on and off states of electricity.

Electricity, which runs through the components of your com- puter and makes it understand and execute your programs, can exist in only two states—on or off. As with a light bulb, electricity is either flowing (it is on) or it is not flowing (it is off). Even though you can dim some lights, the electricity is still either on or off.

Today’s modern digital computers employ this on-or-off con- cept. Your computer is nothing more than millions of on and off switches. You might have heard about integrated circuits, transis- tors, and even vacuum tubes that computers have contained over the years. These electrical components are nothing more than switches that rapidly turn electrical impulses on and off.

This two-state on and off mode of electricity is called a binary state of electricity. Computer people use a 1 to represent an on state (a switch in the computer that is on) and a 0 to represent an off state (a switch that is off). These numbers, 1 and 0, are called binary digits. The term binary digits is usually shortened to bits. A bit is either a 1 or a 0 representing an on or an off state of electricity. Different combinations of bits represent different characters.

Several years ago, someone listed every single character that might be represented on a computer, including all uppercase letters, all lowercase letters, the digits 0 through 9, the many other charac- ters (such as %, *, {, and +), and some special control characters. When you add the total number of characters that a PC can repre- sent, you get 256 of them. The 256 ASCII characters are listed in Appendix C’s ASCII (pronounced ask-ee) table.

The order of the ASCII table’s 256 characters is basically arbi- trary, just as the telegraph’s Morse code table is arbitrary. With Morse code, a different set of long and short beeps represent different letters of the alphabet. In the ASCII table, a different combination of bits (1s and 0s strung together) represent each of the 256 ASCII characters. The ASCII table is a standard table used by almost every PC in the world. ASCII stands for American Standard Code for Information Interchange. (Some minicomputers and main- frames use a similar table called the EBCDIC table.)

It turns out that if you take every different combination of eight 0s strung together, to eight 1s strung together (that is, from 00000000, 00000001, 00000010, and so on until you get to 11111110, and finally, 11111111), you have a total of 256 of them. (256 is 2 to the 8th power.)

Each memory location in your computer holds eight bits each. These bits can be any combination of eight 1s and 0s. This brings us to the following fundamental rule of computers.

To bring this into better perspective, consider that the bit pattern needed for the uppercase letter A is 01000001. No other character in the ASCII table “looks” like this to the computer because each of the 256 characters is assigned a unique bit pattern.

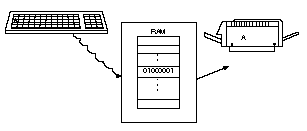Suppose that you press the A key on your keyboard. Your keyboard does not send a letter A to the computer; rather, it looks in its ASCII table for the on and off states of electricity that represent the letter A. As Figure A.3 shows, when you press the A key, the keyboard actually sends 01000001 (as on and off impulses) to the computer. Your computer simply stores this bit pattern for A in a memory location. Even though you can think of the memory loca- tion as holding an A, it really holds the byte 01000001.

Figure A.3. Your computer keeps track of characters by their bit patterns.

If you were to print that A, your computer would not send an A to the printer; it would send the 01000001 bit pattern for an A to the printer. The printer receives that bit pattern, looks up the correct letter in the ASCII table, and prints an A.

From the time you press the A until the time you see it on the printer, it is not a letter A! It is the ASCII pattern of bits that the computer uses to represent an A. Because a computer is electrical, and because electricity is easily turned on and off, this is a nice way for the computer to manipulate and move characters, and it can do so very quickly. Actually, if it were up to the computer, you would enter everything by its bit pattern, and look at all results in their bit patterns. Of course, it would be much more difficult for us to learn to program and use a computer, so devices such as the keyboard, screen, and printer are created to work part of the time with letters as we know them. That is why the ASCII table is such an integral part of a computer.

There are times when your computer treats two bytes as a

single value. Even though memory locations are typically eight bits wide, many CPUs access memory two bytes at a time. If this is the case, the two bytes are called a word of memory. On other computers (commonly mainframes), the word size might be four bytes (32 bits) or even eight bytes (64 bits).

The Order of Bit s

To further understand memory, you should understand how programmers refer to individual bits. Figure A.4 shows a byte and a two-byte word. Notice that the bit on the far right is called bit 0. From bit 0, keep counting by ones as you move left. For a byte, the bits are numbered 0 to 7, from right to left. For a double-byte (a 16- bit word), the bits are numbered from 0 to 15, from right to left.

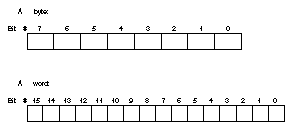
Figure A.4. The order of bits in a byte and a two-byte word.

Bit 0 is called the least-significant bit, or sometimes the low-order bit. Bit 7 (or bit 15 for a two-byte word) is called the most-significant bit, or sometimes the high-order bit.

Binary Number s

Because a computer works best with 1s and 0s, its internal numbering method is limited to a base-2 (binary) numbering system. People work in a base-10 numbering system in the “real” world. The base-10 numbering system is sometimes called the decimal number- ing system. There are always as many different digits as the base in a numbering system. For example, in the base-10 system, there are ten digits, 0 through 9. As soon as you count to 9 and run out of digits, you have to combine some that you already used. The number 10 is a representation of ten values, but it combines the digits 1 and 0.

The same is true of base -2. There are only two digits, 0 and 1. As soon as you run out of digits, after the second one, you have to reuse digits. The first seven binary numbers are 0, 1, 10, 11, 100, 101,

and 110.

It is okay if you do not understand how these numbers were derived; you will see how in a moment. For the time being, you should realize that no more than two digits, 0 and 1, can be used to represent any base-2 number, just as no more than ten digits, 0 through 9, can be used to represent any base-10 number in the regular numbering system.

You should know that a base-10 number, such as 2981, does not really mean anything by itself. You must assume what base it is. You get very used to working with base-10 numbers because you use them every day. However, the number 2981 actually represents a quantity based on powers of 10. For example, Figure A.5 shows what the number 2981 actually represents. Notice that each digit in the number represents a certain number of a power of 10.

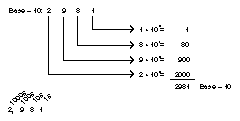
Figure A.5. The base-10 breakdown of the number 2981.

A binary number can contain only the digits 1 and 0.

This same concept applies when you work in a base-2 number- ing system. Your computer does this because the power of 2 is just as common to your computer as the power of 10 is to you. The only difference is that the digits in a base-2 number represent powers of 2 and not powers of 10. Figure A.6 shows you what the binary numbers 10101 and 10011110 are in base-10. This is how you convert any binary number to its base-10 equivalent.

Figure A.6. The base-2 breakdown of the numbers 10101 and 10011110.

A base-2 number contains only 1s and 0s. To convert any base- 2 number to base-10, add each power of 2 everywhere a 1 appears in the number. The base-2 number 101 represents the base-10 number

5. (There are two 1s in the number, one in the 2 to the 0 power, which equals 1, and one in the 2 to the second power, which equals 4.) Table

A.1 shows the first 18 base-10 numbers and their matching base-2 numbers.

You do not have to memorize this table; you should be able to figure the base-10 numbers from their matching binary numbers by adding the powers of two for each 1 (on) bit. Many programmers do memorize the first several binary numbers because it comes in handy in advanced programming techniques.

What is the largest binary number a byte can hold? The answer is all 1s, or 11111111. If you add the first eight powers of 2, you get 255.

A byte holds either a number or an ASCII character, depending on how it is accessed. For example, if you were to convert the base- 2 number 01000001 to a base-10 number, you would get 65. How- ever, this also happens to be the ASCII bit pattern for the uppercase letter A. If you check the ASCII table, you see that the A is ASCII code

65. Because the ASCII table is so closely linked with the bit patterns, the computer knows whether to work with a number 65 or a letter A—by the context of how the patterns are used.

A binary number is not limited to a byte, as an ASCII character is. Sixteen or 32 bits at a time can represent a binary number (and usually do). There are more powers of 2 to add when converting that number to a base-10 number, but the process is the same. By now you should be able to figure out that 1010101010101010 is 43,690 in base- 10 decimal numbering system (although it might take a little time to calculate).

To convert from decimal to binary takes a little more effort. Luckily, you rarely need to convert in that direction. Converting from base-10 to base-2 is not covered in this appendix.

Binary Arithmeti c

At their lowest level, computers can only add and convert binary numbers to their negative equivalents. Computers cannot truly subtract, multiply, or divide, although they simulate these operations through judicious use of the addition and negative- conversion techniques.

If a computer were to add the numbers 7 and 6, it could do so (at the binary level). The result is 13. If, however, the computer were instructed to subtract 7 from 13, it could not do so. It can, however, take the negative value of 7 and add that to 13. Because –7 plus 13 equals 6, the result is a simulated subtraction.

To multiply, computers perform repeated addition. To multi- ply 6 by 7, the computer adds seven 6s together and gets 42 as the answer. To divide 42 by 7, a computer keeps subtracting 7 from 42 repeatedly until it gets to a 0 answer (or less than 0 if there is a remainder), then counts the number of times it took to reach 0.

Because all math is done at the binary level, the following additions are possible in binary arithmetic:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10

Because these are binary numbers, the last result is not the number 10, but the binary number 2. (Just as the binary 10 means “no ones, and carry an additional power of 2,” the decimal number 10 means “no ones, and carry a power of 10.”) No binary digit repre- sents a 2, so you have to combine the 1 and the 0 to form the new number.

Because binary addition is the foundation of all other math, you should learn how to add binary numbers. You will then understand how computers do the rest of their arithmetic.

Using the binary addition rules shown previously, look at the following binary calculations:

01000001 (65 decimal)

+ 00101100 (44 decimal)

01101101 (109 decimal)

The first number, 01000001, is 65 decimal. This also happens to be the bit pattern for the ASCII A, but if you add with it, the computer interprets it as the number 65 rather than the character A.

The following binary addition requires a carry into bit 4 and

bit 6:

00101011 (43 decimal)

+ 00100111 (39 decimal)

01010010 (82 decimal)

Typically, you have to ignore bits that carry past bit 7, or bit 15 for double-byte arithmetic. For example, both of the following

binary additions produce incorrect positive results:

10000000 (128 decimal) 1000000000000000

(65536 decimal)

+ 10000000 (128 decimal) +1000000000000000

00000000 (0 decimal) (65536 decimal)

0000000000000000

(0 decimal)

There is no 9th or 17th bit for the carry, so both of these seem to produce incorrect results. Because the byte and 16-bit word cannot hold the answers, the magnitude of both these additions is not possible. The computer must be programmed, at the bit level, to perform multiword arithmetic, which is beyond the scope of this book.

Negative binary

Binary Negative Number s

Because subtracting requires understanding binary negative numbers, you need to learn how computers represent them. The computer uses 2’s complement to represent negative numbers in binary form. To convert a binary number to its 2’s complement (to

numbers are stored

in their 2’s complement format.

its negative) you must:

1. Reverse the bits (the 1s to 0s and the 0s to 1s).

2. Add 1.

This might seem a little strange at first, but it works very well for binary numbers. To represent a binary –65, you have to take the binary 65 and convert it to its 2’s complement, such as

01000001 (65 decimal) 10111110 (Reverse the bits)

+1 (Add 1)

10111111 (–65 binary)

By converting the 65 to its 2’s complement, you produce –65 in binary. You might wonder what makes 10111111 mean –65, but by the 2’s complement definition it means –65.

If you were told that 10111111 is a negative number, how would you know which binary number it is? You perform the 2’s complement on it. Whatever number you produce is the positive of that negative number. For example:

10111111 (–65 decimal) 01000000 (Reverse the bits)

+1 (Add 1)

01000001 (65 decimal)

Something might seem wrong at this point. You just saw that 10111111 is the binary –65, but isn’t 10111111 also 191 decimal (adding the powers of 2 marked by the 1s in the number, as explained earlier)? It depends whether the number is a signed or an unsigned number. If a number is signed, the computer looks at the most-significant bit (the bit on the far left), called the sign bit. If the most-significant bit is a 1, the number is negative. If it is 0, the number is positive.

Most numbers are 16 bits long. That is, two-byte words are used to store most integers. This is not always the case for all computers, but it is true for most PCs.

In the C++ programming language, you can designate num- bers as either signed integers or unsigned integers (they are signed by default if you do not specify otherwise). If you designate a variable as a signed integer, the computer interprets the high-order bit as a sign bit. If the high-order bit is on (1), the number is negative. If the high-order bit is off (0), the number is positive. If, however, you designate a variable as an unsigned integer, the computer uses the high-order bit as just another power of 2. That is why the range of unsigned integer variables goes higher (generally from 0 to 65535, but it depends on the computer) than for signed integer variables (generally from –32768 to +32767).

After so much description, a little review is in order. Assume that the following 16-bit binary numbers are unsigned:

0011010110100101

1001100110101010

1000000000000000

These numbers are unsigned, so the bit 15 is not the sign bit, but simply another power of 2. You should practice converting these large 16-bit numbers to decimal. The decimal equivalents are

13733

39338

32768

If, on the other hand, these numbers are signed numbers, the high-order bit (bit 15) indicates the sign. If the sign bit is 0, the numbers are positive and you convert them to decimal in the usual manner. If the sign bit is 1, you must convert the numbers to their 2’s complement to find what they equal. Their decimal equivalents are

+13733

–26198

–32768

To compute the last two binary numbers to their decimal equivalents, take their 2’s complement and convert it to decimal. Put a minus sign in front of the result and you find what the original number represents.

Hexadecimal numbers use 16

unique digits, 0 through F.

Hexadecimal Number s

All those 1s and 0s get confusing. If it were up to your com- puter, however, you would enter everything as 1s and 0s! This is unacceptable to people because we do not like to keep track of all those 1s and 0s. Therefore, a hexadecimal numbering system (some- times called hex) was devised. The hexadecimal numbering system is based on base-16 numbers. As with other bases, there are 16 unique digits in the base-16 numbering system. Here are the first 19 hexadecimal numbers:

0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12

Because there are only 10 unique digits (0 through 9), the letters A through F represent the remaining six digits. (Anything could have been used, but the designers of the hexadecimal numbering system decided to use the first six letters of the alphabet.)

To understand base-16 numbers, you should know how to convert them to base-10 so they represent numbers with which people are familiar. Perform the conversion to base-10 from base-16 the same way you did with base-2, but instead of using powers of 2, represent each hexadecimal digit with powers of 16. Figure A.7 shows how to convert the number 3C5 to decimal.

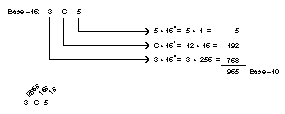
Figure A.7. Converting hexadecimal 3C5 to its decimal equivalent.

You should be able to convert 2B to its decimal 43 equivalent, and E1 to decimal 225 in the same manner. Table A.2 shows the first 20 decimal, binary, and hexadecimal numbers.

Table A.2. The first 20 base-10, base-2 (binary), and base-16 (hexadecimal) numbers.

Why Learn Hexadecimal ?

Because of its close association to the binary numbers your computer uses, hexadecimal notation is extremely efficient for de- scribing memory locations and values. It is much easier for you (and more importantly at this level, for your computer) to convert from base-16 to base-2 than from base-10 to base-2. Therefore, you some- times want to represent data at the bit level, but using hexadecimal notation is easier (and requires less typing) than using binary numbers.

To convert from hexadecimal to binary, convert each hex digit to its four-bit binary number. You can use Table A.2 as a guide for this. For example, the following hexadecimal number

5B75

can be converted to binary by taking each digit and converting it to four binary numbers. If you need leading zeroes to “pad” the four digits, use them. The number becomes

0101 1011 0111 0101

It turns out that the binary number 0101101101110101 is exactly equal to the hexadecimal number 5B75. This is much easier than converting them both to decimal first.

To convert from binary to hexadecimal, reverse this process. If you were given the following binary number

1101000011110111111010

you could convert it to hexadecimal by grouping the bits into groups of four, starting with the bit on the far right. Because there is not an even number of groups of four, pad the one on the far left with zeroes. You then have the following:

0011 0100 0011 1101 1111 1010

Now you only have to convert each group of four binary digits into their hexadecimal number equivalent. You can use Table A.2 to help. You then get the following base-16 number:

343DFA

The C++ programming language also supports the base-8 octal representation of numbers. Because octal numbers are rarely used with today’s computers, they are not covered in this appendix.

How Binary and Addressin g Relate to C+ +

The material presented here may seem foreign to many pro- grammers. The binary and 2’s complement arithmetic reside deep in your computer, shielded from most programmers (except assem- bly-language programmers). Understanding this level of your com- puter, however, makes everything else you learn seem more clear.

Many C++ programmers learn C++ before delving into binary and hexadecimal representation. For those programmers, much about the C++ language seems strange, but it could be explained very easily if they understood the basic concepts.

For example, a signed integer holds a different range of num- bers than an unsigned integer. You now know that this is because the sign bit is used in two different ways, depending on whether the number is designated as signed or unsigned.

The ASCII table (see Appendix C) also should make more sense to you after this discussion. The ASCII table is an integral part of your computer. Characters are not actually stored in memory and variables; rather, their ASCII bit patterns are. That is why C++ can move easily between characters and integers. The following two C++ statements are allowed, whereas they probably would not be in another programming language:

char c = 65; / / Pl aces t he ASCI I l ett er A i n c. i nt ci = ‘ A’ ; / / Pl aces t he number 65 i n ci .

The hexadecimal notation also makes much more sense if you truly understand base-16 numbers. For example, if you see the following line in a C++ program

char a = ‘ \ x041’ ;

you could convert the hex 41 to decimal (65 decimal) if you want to know what is being assigned. Also, C++ systems programmers find that they can better interface with assembly-language programs when they understand the concepts presented in this appendix.

If you gain only a cursory knowledge of this material at this point, you will be very much ahead of the game when you program in C++!