Multidimensional Arrays

Some data fits in lists, such as the data discussed in the previous two chapters, and other data is better suited for tables of information. This chapter takes arrays one step further. The previous chapters introduced single-dimensional arrays; arrays that have only one subscript and represent lists of values.

This chapter introduces arrays of more than one dimension, called multidimensional arrays. Multidimensional arrays, sometimes called tables or matrices, have at least two dimensions (rows and columns). Many times they have more than two.

This chapter introduces the following concepts:

• Multidimensional arrays

• Reserving storage for multidimensional arrays

• Putting data in multidimensional arrays

• Using nested f or loops to process multidimensional arrays

If you understand single-dimensional arrays, you should have no trouble understanding arrays that have more than one dimen- sion.

Multidimensional Arra y Basics

A multidimensional array has more than one subscript.

A multidimensional array is an array with more than one subscript. Whereas a single-dimensional array is a list of values, a multidimensional array simulates a table of values, or multiple tables of values. The most commonly used table is a two- dimensional table (an array with two subscripts).

Suppose a softball team wanted to keep track of its players’ batting records. The team played 10 games, and there are 15 players on the team. Table 25.1 shows the team’s batting record.

Table 25.1. A softball team’s batting record.

A three-dimensional table has three dimensions: depth, rows, and columns.

Do you see that the softball table is a two-dimensional table? It has rows (the first dimension) and columns (the second dimension). Therefore, this is called a two-dimensional table with 15 rows and 10 columns. (Generally, the number of rows is specified first.)

Each row has a player’s name, and each column has a game number associated with it, but these are not part of the actual data. The data consists of only 150 values (15 rows by 10 columns). The data in a two-dimensional table always is the same type of data; in this case, every value is an integer. If it were a table of salaries, every element would be a floating-point decimal.

The number of dimensions, in this case two, corresponds to the dimensions in the physical world. The single-dimensioned array is a line, or list of values. Two dimensions represent both length and width. You write on a piece of paper in two dimensions; two dimensions represent a flat surface. Three dimensions represent width, length, and depth. You have seen 3-D movies. Not only do the images have width and height, but they also seem to have depth. Figure 25.1 shows what a three-dimensional array looks like if it has a depth of four, six rows, and three columns. Notice that a three- dimensional table resembles a cube.

It is difficult to visualize more than three dimensions. How- ever, you can think of each dimension after three as another occur- rence. In other words, a list of one player’s season batting record can be stored in an array. The team’s batting record (as shown in Table 25.1) is two-dimensional. The league, made of up several teams’ batting records, represents a three-dimensional table. Each team (the depth of the table) has rows and columns of batting data. If there is more than one league, it is another dimension (another set of data). C++ enables you to store several dimensions, although “real-

world” data rarely requires more than two or three.

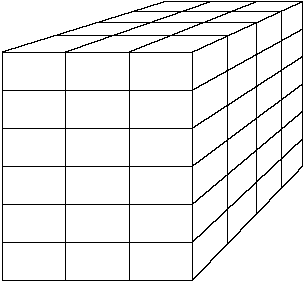6 rows

Figure 25.1. Representing a three-dimensional table (a cube).

Reserving Multidimensiona l Arrays

When you reserve a multidimensional array, you must inform C++ that the array has more than one dimension by putting more than one subscript in brackets after the array name. You must put a separate number, in brackets, for each dimension in the table. For example, to reserve the team data from Table 25.1, you use the following multidimensional array declaration.

Declare an integer array called t eams with 15 rows and 10 columns.

i nt t eams[ 15][ 10] ; / / Reser ves a t wo- di mensi onal t abl e.

Properly reserving the t eams table produces a table with 150 elements. Figure 25.2 shows what each element’s subscript looks like.

columns

rows

Figure 25.2. Subscripts for the softball team table.

The far-right dimension always represents columns, the next represents rows, and so on.

If you had to track three teams, each with 15 players and 10 games, the three-dimensional table would be created as follows:

i nt t eams[ 3][ 15][ 10] ; / / Reser ves a t hr ee- di mensi onal t abl e.

When creating a two-dimensional table, always put the maxi- mum number of rows first, and the maximum number of columns second. C++ always uses 0 as the starting subscript of each dimen- sion. The last element, the lower-right element of the t eams table, is t eams[ 2] [ 14] [ 9] .

Examples

1. Suppose

   you wanted to keep track of utility bills for the year. You can store 12 months of four utilities in a two- dimensional table of floating-point amounts, as the follow- ing array declaration demonstrates:

f l oat ut ili t i es[ 12][ 4] ; / / Reser ves 48 el ement s.

You can compute the total number of elements in a multi- dimensional array by multiplying the subscripts. Because 12 times 4 is 48, there are 48 elements in this array (12 rows, 4 columns). Each of these elements is a floating-point data type.

1. If

   you were keeping track of five years’ worth of utilities, you have to add an extra dimension. The first dimension is the years, the second is the months, and the last is the indi- vidual utilities. Here is how you reserve storage:

f l oat ut ili t i es[ 5][ 12][ 4] ; / / Reser ves 240 el ement s.

Mapping Arrays to Memor y

C++ approaches multidimensional arrays a little differently than most programming languages do. When you use subscripts, you do not have to understand the internal representation of multi- dimensional arrays. However, most C++ programmers think a deeper understanding of these arrays is important, especially when programming advanced applications.

A two-dimensional array is actually an array of arrays. You program multidimensional arrays as though they were tables with rows and columns. A two-dimensional array is actually a single- dimensional array, but each of its elements is not an integer, floating- point, or character, but another array.

Knowing that a multidimensional array is an array of other arrays is critical when passing and receiving such arrays. C++ passes all arrays, including multidimensional arrays, by address. Suppose you were using an integer array called scor es , reserved as a 5-by-6 table. You can pass scor es to a function called pr i nt _i t () , as follows:

pr i nt _i t ( scor es) ; / / Passes t abl e t o a f unct i on.

The function pr i nt _i t () has to identify the type of parameter being passed to it. The pr i nt _i t () function also must recognize that the parameter is an array. If scor es were one-dimensional, you could receive it as

pr i nt _i t ( i nt scor es[] ) / / Wor ks onl y i f scor es

/ / i s one- di mensi onal .

or

pr i nt _i t ( i nt scor es[ 10] ) / / Assumi ng scor es

/ / has 10 el ement s.

If scor es were a multidimensional table, you would have to designate each pair of brackets and put the maximum number of subscripts in its brackets, as in

pr i nt _i t ( i nt scor es[ 5][ 6] ) / / I nf orm pr i nt _i t () of

/ / t he arr ay’ s di mensi ons.

or

pr i nt _i t ( i nt scor es[][ 6] ) / / I nf orm pr i nt _i t () of

/ / t he arr ay’ s di mensi ons.

Notice you do not have to explicitly state the maximum sub- script on the first dimension when receiving multidimensional

arrays, but you must designate the second. If scor es were a three- dimensional table, dimensioned as 10 by 5 by 6, you would receive it with pr i nt _i t () as

pr i nt _i t ( i nt scor es[][ 5][ 6] ) / / Onl y f i r st di mensi on

/ / i s opt i onal .

or

C++ stores multidimensional arrays in row order.

pr i nt _i t ( i nt scor es[ 10][ 5][ 6] ) / / I nf orm pr i nt _i t () of

/ / arr ay’ s di mensi ons.

You should not have to worry too much about the way tables are physically stored. Even though a two-dimensional table is actually an array of arrays (and each of those arrays contains another array if it is a three-dimensional table), you can use subscripts to program multidimensional arrays as if they were stored in row-and- column order.

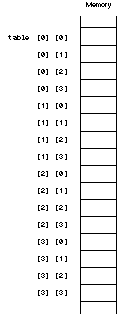
Multidimensional arrays are stored in row order. Suppose you want to keep track of a 3-by-4 table. The top of Figure 25.3 shows how that table (and its subscripts) are visualized. Despite the two-dimensional table organization, your memory is still sequen- tial storage. C++ has to map multidimensional arrays to single- dimensional memory, and it does so in row order.

Each row fills memory before the next row is stored. Figure 25.3 shows how a 3-by-4 table is mapped to memory.

The entire first row (t abl e[ 0][ 0] through t abl e[ 0][ 3] ) is stored first in memory before any of the second row. A table is actually an array of arrays, and, as you learned in previous chapters, array elements are always stored sequentially in memory. Therefore, the first row (array) completely fills memory before the second row. Figure 25.3 shows how two-dimensional arrays map to memory.

Defining Multidimensiona l Arrays

C++ is not picky about the way you define a multidimensional array when you initialize it at declaration time. As with single- dimensional arrays, you initialize multidimensional arrays with

braces that designate dimensions. Because a multidimensional ar- ray is an array of arrays, you can nest braces when you initialize them.

First row

Second row

Third row

Fourth row

Figure 25.3. Mapping a two-dimensional table to memory.

The following three array definitions fill the three arrays ar a1 ,

ar a2 , and ar a3 , as shown in Figure 25.4:

i nt ar a1[ 5] = { 8, 5, 3, 25, 41} ; / / One- di mensi onal arr ay. i nt ar a2[ 2][ 4] ={{ 4, 3, 2, 1} , { 1, 2, 3, 4}} ;

i nt ar a3[ 3][ 4] ={{ 1, 2, 3, 4} , { 5, 6, 7, 8} , { 9, 10, 11, 12}} ;

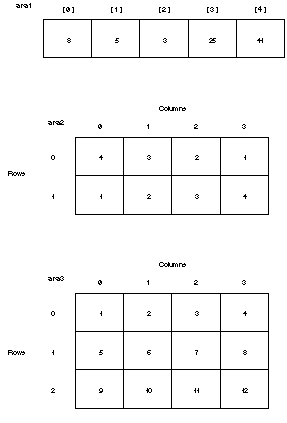
Figure 25.4. After initializing a table.

Notice that the multidimensional arrays are stored in row order. In ar a3 , the first row receives the first four elements of the definition (1, 2, 3, and 4).

You can initialize a multidimensional array as if it were single- dimensional in C++. You must keep track of the row order if you do this. For instance, the following two definitions also reserve storage for and initialize ar a2 and ar a3 :

i nt ar a2[ 2][ 4] ={ 4, 3, 2, 1, 1, 2, 3, 4} ;

i nt ar a3[ 3][ 4] ={ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13} ;

There is no difference between initializing ar a2 and ar a3 with or without the nested braces. The nested braces seem to show the dimensions and how C++ fills them a little better, but the choice of using nested braces is yours.

One last point to consider is how multidimensional arrays are viewed by your compiler. Many people program in C++ for years, but never understand how tables are stored internally. As long as you use subscripts, a table’s internal representation should not matter. When you learn about pointer variables, however, you might want to know how C++ stores your tables in case you want to reference them with pointers (as shown in the next few chapters).

Figure 25.5 shows the way C++ stores a 3-by-4 table in memory. Unlike single-dimensional arrays, each element is stored contigu- ously, but notice how C++ views the data. Because a table is an array of arrays, the array name contains the address of the start of the primary array. Each of those elements points to the arrays it contains (the data in each row). This coverage of table storage is for your information only, at this point. As you become more proficient in C++, and write more powerful programs that manipulate internal memory, you might want to review this table storage method.

Tables and f or Loop s

As the following examples show, nested f or loops are useful when you want to loop through every element of a multidimen- sional table.

For instance, the section of code,

f or (r ow=0; r ow<2; r ow++)

{ f or ( col =0; col <3; col ++)

{ cout << r ow << “ “ << col “ \ n” ; }

}

produces the following output:

ar a name

An array of arrays

First row

Second row

Third row

Fourth row

Figure 25.5. Internal representation of a two-dimensional table.

Nested loops work well with multi- dimensional arrays.

These numbers are the subscripts, in row order, for a two-row by three-column table dimensioned with

i nt t abl e[ 2][ 3];

Notice there are as many f or loops as there are subscripts in the array (two). The outside loop represents the first subscript (the rows), and the inside loop represents the second subscript (the columns). The nested f or loop steps through each element of the table.

You can use ci n , get s() , get , and other input functions to fill a table, and you also can assign values to the elements when declaring the table. More often, the data comes from data files on the disk. Regardless of what method stores the values in multidimensional arrays, nested f or loops are excellent control statements to step through the subscripts. The following examples demonstrate how nested f or loops work with multidimensional arrays.

Examples

1. The

   following statements reserve enough memory elements for a television station’s ratings (A through D) for one week:

char r at i ngs[ 7][ 48];

These statements reserve enough elements to hold seven days (the rows) of ratings for each 30-minute time slot (48 of them in a day).

Every element in a table is always the same type. In this case, each element is a character variable. Some are initialized with the following assignment statements:

shows[ 3][ 12] = ‘ B’ ; / / St or es B i n 4t h r ow, 13t h col umn. shows[ 1][ 5] = ‘ A’ ; / / St or es C i n 2nd r ow, 6t h col umn. shows[ 6][ 20] = get ch() ; / / St or es t he l ett er t he user t ypes.

1. A computer company sells two sizes of disks: 3 1/ 2-inch and 5 1/

   4-inch. Each disk comes in one of four capacities: single- sided double-density, double-sided double-density, single- sided high-density, and double-sided high-density.

The disk inventory is well-suited for a two-dimensional table. The company determined that the disks have the following retail prices:

Double Density High Density

The company wants to store the price of each disk in a table for easy access. The following program stores the prices with assignment statements.

/ / Fil ename: C25DI SK1. CPP

/ / Assi gns di sk pr i ces t o a t abl e. #i ncl ude <i ost r eam. h>

#i ncl ude <i omani p. h> voi d mai n()

{

f l oat di sks[ 2][ 4] ; / / Tabl e of di sk pr i ces. i nt r ow, col ; / / Subscr i pt var i abl es.

/ / Pr i nt t he pr i ces.

f or (r ow=0; r ow<2; r ow++)

{ f or ( col =0; col <4; col ++)

{ cout << “ $” << set pr eci si on( 2) <<

di sks[ r ow][ col ] << “ \ n” ; }

}

r et ur n;

}

This program displays the prices as follows:

$2. 39

$2. 75

$3. 29

$3. 59

$1. 75

$2. 19

$2. 69

$2. 95

It prints them one line at a time, without any descriptive titles. Although the output is not labeled, it illustrates how you can use assignment statements to initialize a table, and how nested f or loops can print the elements.

1. The

   preceding disk inventory would be displayed better if the output had descriptive titles. Before you add titles, it is helpful for you to see how to print a table in its native row and column format.

Typically, you use a nested f or loop, such as the one in the previous example, to print rows and columns. You should not output a newline character with every cout , however. If you do, you see one value per line, as in the previous program’s output, which is not the row and column format of the table.

You do not want to see every disk price on one line, but you want each row of the table printed on a separate line. You must insert a cout << “ \ n” ; to send the cursor to the next line each time the row number changes. Printing newlines after each row prints the table in its row and column format, as this program shows:

/ / Fil ename: C25DI SK2. CPP

/ / Assi gns di sk pr i ces t o a t abl e

/ / and pr i nt s t hem i n a t abl e f ormat. #i ncl ude <i ost r eam. h>

#i ncl ude <i omani p. h> voi d mai n()

{

f l oat di sks[ 2][ 4] ; / / Tabl e of di sk pr i ces. i nt r ow, col ;

/ / Pr i nt t he pr i ces

f or (r ow=0; r ow<2; r ow++)

{ f or ( col =0; col <4; col ++)

{ cout << “ $” << set pr eci si on( 2) <<

di sks[ r ow][ col ] << “ \t ” ;

}

cout << “ \ n” ; / / Pr i nt s a new li ne aft er each r ow.

}

r et ur n;

}

Here is the output of the disk prices in their native table order:

1. To add the titles, simply print a row of titles before the first row

   of values, then print a new column title before each column, as shown in the following program:

/ / Fil ename: C25DI SK3. CPP

/ / Assi gns di sk pr i ces t o a t abl e

/ / and pr i nt s t hem i n a t abl e f ormat wi t h t i t l es. #i ncl ude <i ost r eam. h>

#i ncl ude <i omani p. h>

voi d mai n()

{

f l oat di sks[ 2][ 4] ; / / Tabl e of di sk pr i ces. i nt r ow, col ;

/ / Pr i nt t he col umn t i t l es.

cout << “ \t Si ngl e- si ded\t Doubl e- si ded\t Si ngl e- si ded\t ” << “ Doubl e- si ded\ n” ;

cout << “ \t Doubl e- densi t y\t Doubl e- densi t y\t Hi gh- densi t y” << “ \t Hi gh- densi t y\ n” ;

/ / Pr i nt t he pr i ces

f or (r ow=0; r ow<2; r ow++)

{ i f (r ow == 0)

{ cout << “ 3- 1/ 2\ ” \t ” ; } / / Need \ ” t o

/ / pr i nt quot at i on.

el se

{ cout << “ 5- 1/ 4\ ” \t ” ; }

f or ( col =0; col <4; col ++) / / Pr i nt t he curr ent r ow.

{ cout << set pr eci si on( 2) << “ $” << di sks[ r ow][ col ]

<< “ \t\t ” ;

}

cout << “ \ n” ; / / Pr i nt a newli ne aft er each r ow.

}

r et ur n;

}

Here is the output from this program:

Review Question s

The answers to the review questions are in Appendix B.

1. What

   statement reserves a two-dimensional table of integers called scor es with five rows and six columns?

2. What statement reserves a three-dimensional table of four character

   arrays called i ni t i al s with 10 rows and 20 columns?

3. In the following statement, which subscript (first or second)

   represents rows and which represents columns?

i nt wei ght s[ 5][ 10];

1. How

   many elements are reserved with the following statement?

i nt ar a[ 5][ 6];

1. The following table of integers is called ar a :

What values do the following elements contain? a. ar a[ 2] [ 2]

b. ar a[ 0] [ 1]

c. ar a[ 2] [ 3]

d. ar a[ 2] [ 4]

1. What

   control statement is best for stepping through multi- dimensional arrays?

2. Notice the following section of a program:

i nt gr ades[ 3][ 5] = { 80, 90, 96, 73, 65, 67, 90, 68, 92, 84, 70,

55, 95, 78, 100} ;

What are the values of the following:

1. grades[ 2] [ 3]

2. grades[ 2] [ 4]

3. grades[ 0] [ 1]

Review Exercise s

1. Write

   a program that stores and prints the numbers from 1 to 21 in a 3-by-7 table. (Hint: Remember C++ begins sub- scripts at 0.)

2. Write a program that reserves storage for three years’ worth of

   sales data for five salespeople. Use assignment statements to fill the table with data, then print it, one value per line.

3. Instead

   of using assignment statements, use the ci n function to fill the salespeople data from Exercise 2.

4. Write a program that tracks the grades for five classes, each having

   10 students. Input the data using the ci n function. Print the table in its native row and column format.

Summary

You now know how to create, initialize, and process multidi- mensional arrays. Although not all data fits in the compact format of tables, much does. Using nested f or loops makes stepping through a multidimensional array straightforward.

One of the limitations of a multidimensional array is that each element must be the same data type. This keeps you from being able to store several kinds of data in tables. Chapter 28, “Structures,” shows you how to store data in different ways to overcome this limitation.