三、伽罗瓦与群论
群论这门数学在当代已经成为数学中的重要部分了,而其理论的应用、发展应该首先归功于埃瓦里斯特·伽罗瓦。因为是伽罗瓦赋予群论以实在的内容,建立起群论学并加以完善,从而改变了 19 世纪初叶,数学科学发展的停滞状况,开创了新的繁荣时期。所以说,伽罗瓦对科学的重大贡献就在于他对群论的贡献。因此,要了解伽罗瓦,就必须了解群论。
- 群的重要
解方程式是数学中一件重要的事情。代数方程式可以依他的次数来分类。
一次方程式 ax+b=0 的解答很容易得出,是x=-b/a
二次方程式ax2+bx+c=0 的解是
x=( - b± b2 - 4ac)/2a
但是,三次方程式ax3+bx2+cx+d=0 和四次方程式
ax4+ bx3+cx2+ dx+e= 0
的解法就比解一次、二次方程式难得多了,直到 16 世纪才有了解法。当方程式的次数增大时,解法的困难增加得很快。一般数学家虽都不会
解高于四次的方程式,却都相信一定是能办到的。直到 19 世纪,利用群论的道理,才证明了这是不可能的事。因为一个问题能否解决要看对于解答所加的限制条件而定。譬如
x+5=3
如果允许 x 为负数的话,此方程可解;若限定 x 不能是负数,则此方程式就不能解了。同样,假如 x 表示饼数,方程式
2x+3=10
是可解的。但倘若x表示人数、这个方程式就不能解了,因为 x=3 1 (人)
2
没有意义。
再如,一个代数式可以分解因数或不可以分解因数要看是在什么数域对它进行分解。如
x2+1
在实数域中是不可分解的,可是在复数域却是可分的,因为x2+1=(x+i)(x-i),
其中i=
由于一般高于四次的方程式不能用根式解,即它的根不能用有限次的有理运算(加、减、乘、除)和开方表作方程式的系数的函数,所以说高于四次的方程不能解。
- 群的内容数学中的系统可以说是一部数学的机器,它的主要部分是
-
元素。
-
相对应的运算。例如:
- ①元素是一切整数(正整数、负整数或 0);
②运算是加法。
- ①元素是一切有理数(可以写成两个整数的商的数,如 3/4。 0 除外);
②运算是乘法。
(C)①元素是某几个文字(如 x1、x2、x3)的置换;
②运算是将一个置换跟着另一个置换。
①元素是下图的旋转,转的度数是 600 或 600 的倍数;
②运算是将一个旋转跟着另一个旋转。
如果这种系统能满足下列四个性质,就称为群。
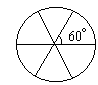
- 假使两个元素用规定的运算结合时,所得的结果仍是系统中的一个元素。
例如:
在(a)中,一个整数加上另一个整数的所得还是一个整数。
在(c)中,假设有一个置换,将 x1 代作 x2,x2 代作 x3,x3 为代作 x1, 即将
x1、x2、x3
换作
x2 x3 x1
置换后的结果仍在原系统中。
- 系统中必须含有主元素。主元素具有与系统中任意另一个元素结合的结果仍是那另一个元素的性质。
例如:
在(a)中,主元素是 0,因为 0 与任何整数相加的结果还是那个整数。在(b)中,主元素是 1,因为任意一个有理数乘以 1 后的积还是自身。在(c)中,主元素是那个将 x1 代作 x1,x2 代作 x2,x3 代作 x3 的置换,
因为任何置换和自身结合的结果是不变的。
在(d)中,主元素是那个 360°的旋转,因为系统中的任意一个旋转和此旋转结合的结果仍为自身。
- 每个元素必须有一个逆元素,即一个元素和其逆元素用系统中的运算结合的结果是主元素。
例如:
在(a)中,3 的逆元素是-3,因为 3 加-3 的和是 0。
在(b)中,a/b 的逆元素是 b/a,因为 a/b 和 b/a 相乘的积是 1。在(C)中,将 x1 代作 x2,x2 代作 x3,x3 代作 x1 的置换的逆元素是将 x2
代作 x1,x3 代作 x2,x1 代作 x3 的置换。因为这两个置换结合的结果是那个将x2 代作 x2,x3 代作 x3,x1 代作 x1 的置换。
在(d)中,60°的旋转(按顺时针方向)的逆元素是一个-60°的旋转
(按逆时针方向)。因为这两个旋转结合的结果是主元素——360°的旋转。
- 结合律必须成立。
例如,设 a,b,c 是任意三个元素,又设运算用记号 O 表示,则结合律
指
(aOb)Oc=aO(bOc) 应用到系统(a)中,为
(3+4)+ 5=3+(4+ 5) 所以结合律在(a)中能成立。
对于一个系统,它是否成群,不但要看它的元素,还要看它的运算才能
决定。
- 群的重要性质
伽罗瓦用来解方程式的置换群具有十分有趣的性质。
在表示置换时,为了方便起见而采取一种简单的记法,即在记 x1,x2, x3 时可将 x 省去,只用 1,2,3 来表示。例如一个将 x1 代作 x2,x2 代作 x3, x3 代作 x1 的置换,可以简单的记作( 1 2 3)
这个记号的意思是说:
1 变作 2,2 变作 3,3 变作 1。换句话说,就是
x1 变作 x2,x2 变作 x3,x3 变作 x1。
同样,(1 3 2 )则表示一个将 x1 变作 x3,x3 变作 x2,x2 变作 x1 的置换。又如
(1 3)(2)或(1 3)
表示一个将 x1 代作 x3,x3 代作 x1,x2 代作 x2 的置换。
有时一个群的部分元素自己形成一群,这种群称为“约群”。例如,前面(a)例中,一切整数对于加法而言,为一群。若单拿一切偶数来看,对于加法,他们也成一群;因为群的四个性质它都适合:
(1)两个偶数的和还是偶数。
(2)0 是主元素。
-
一个正偶数有相应的负偶数作逆元素,而一个负偶数的逆元素是正偶数。
-
结合律成立。
所以,偶数群是整数群的约群。
伽罗瓦证明了约群的元素个数是原来的群的元素个数的约数。
在约群中,最重要的是“不变约群”,即一个约群中的任何元素应用原来的群中任何元素的变形,[例如设有一个元素(1 2 ),用另一个元素(1 2
3)去右乘它,再用(1 2 3)的逆元素(1 3 2)去左乘它,所得的结果是
(1 3 2)(1 2)(1 2 3)=(2 3),
这个结果(2 3)就称为(1 2)应用(1 2 3)的变形。]若仍是约群中的元素,这个约群就称为原来那个群的不变约群。
一个群可以看作是它自己的约群,但不是真约群,一个真约群必须比原来的群小。但如果 H 是 G 的不变约群,假如 G 中没有包含 H 而较 H 大的不变真约群存在时,H 就称为 G 的一个极大不变真约群。
假设 G 是一个群,H 是 G 的一个极大不变真约群,K 是 H 的一个极大不变真的约群,⋯⋯若将 G 的元素用 H 的元素个数去除,H 的元素用 K 的元素个数去除,⋯⋯所得诸数,称为群 G 的“组合因数”。若这些组合因数都是质数,则 G 是一个“可解数”。
在有些群中,群中的一切元素都是某一个元素(主元素例外)的乘幂。如在群
1,(1 2 3),(1 3 2)
中,(1 2 3)2=(1 2 3)(1 2 3)
=(1 3 2)
(1 2 3)3=(1 2 3) (1 2 3)(1 2 3)=1
此群中的元素都是(1 2 3)的乘幂。这种群,称为“巡回群”。
在一个置换群中,若每个文字都有一个而且只有一个置换将这文字换成其他某个文字,则这个群称为“正置换群”。例如群
1,(1 2 3),(1),
在 1 中 x1,变成 x1,在(1 2 3)中 x1 变成 x2,在(1 32)中 x1 变成 x3⋯⋯所以这是一个“巡回正置换群”。
- 一个方程式的群
对于一个一定的数域,每个方程式都有一个群。譬如三次方程式ax3+bx2+cx+d=0,
假定它的三个根 x1,x2,x3 是相异的。任意取一个这三个根的函数,如
x1x2+x3
在这个函数中,若把这些 x 互相替换,那么,会有六种置换。(1 2 )一类的置换为 x2x1+x3;( 1 3)为 x3x2+x1;( 12 3)为 x2x3+x1。此外,还有不动置换。也就是说共有:
1,(1 2),(1 3),(2 3),(1 2 3)(1 3 2)六个置换, 即对于这三个 x,一共有 3!(表示 3×2×1)种可能的置换。一般说,n! 表示 n(n-1(n-2)⋯⋯1,所以 n 个 x 有 n!种置换。于是,伽罗瓦得出
结论,在函数 v1=m1x1+m2x2=m3x3+⋯⋯mnxn 中,当 x 作各种可能的置换时, 这函数就有 n!个不同的值,用 v1,v2,v3,⋯⋯vn!表示这些不同的值, 可作出式子 P(y)=(Y-v1)(Y-v2)⋯⋯(Y-vn!),其中 Y 是一个变数。
将 P(y)的各因子乘出来,就得到一个 Y 的多项式。假设 P(y)在某一数域中分解因数,包含 v1 而在此数域中为不可约的部分是(Y-v1)(Y- v2)或 Y2-(v1+v2)Y+v1v2 在这部分中所含的 v 仅有 v1v2。则将 v1,v2 互相交换的 x 的置换成一群,这个群叫“方程式在这数域中的群”。
一般地说,一个方程式在一定数域中的群是由 P(Y)中包含 v1 的不可约
部分而决定的。将这个不可约部分记作 G(y),则 G(y)=0,这称为“伽罗瓦分解式”。
在一个数域中将一个式子分解因数,到了不能再分解时,若将数域扩大, 可以继续分解下去。但扩大数域的结果是使方程的群变小。
明白什么是方程式在一个数域中的群,就可以去求它。例如二次方程式X2+3X+1= 0
有两个根 x1,x2,可能的置换只有 1 和(1 2)两种。所以它的群或者含有这两个置换或者只有 1 这一个。而这要看是在什么数域中了。
以函数 x1-x2 为例,二次方程式
x2+bx+c= 0 的两根之差是x1 - x2 =
在此例中,规定 b=3,c=1,则
x1 -x2 =
如果所讨论的数域是有理数域,那么,这个函数的值不在数域中,所以群中必有一个置换能变更此函数的值,这就是( 1 2)置换。则此方程式在有理数域中的群是由
1,( 1 2)
两个置换作成的。但如果讨论的数域是实数域,那么,在此数域中,所以群中一切置换都不改变函数 x1-x2 的值,所以(1 2)不能在群中。此方程式在实数域中的群是由 1 一个置换作成的。
- 伽罗瓦的鉴定
伽罗瓦证明了:一个方程式在一个含有它的系数的数域中的群若是“可解群”,则此方程式是可能用根式解的,而且仅在这样的条件下方程式才能用根式解。
以一般二次方程ax2+ bx+c=0
为例,它的两个根是 x1,x2。它在一个含有它的系数的数域中的群之元
素是 1 和(1 2)。这个群的唯一的极大不变真约群是 1,则此群的组合因数是: 2/1= 2,这是一个质数,因此,根据枷罗瓦的鉴定,凡二次方程式都是可用根式解的。
再取一般三次方程ax3+bx2+cx+d=0
来看,因为它有三个根 x1,x2,x3,所以在一个含有它的系数的数域中, 它的群含有 1,(1 2),(1 3),(2 3),(1 2 3),(1 3 2) 六个置换。此群的唯一极大不变真约群含有 1,(1 2 3),(1 3 2)三个置换。据此可知,组合因数是 6/3=2 与 3/1=3,两个都是质数。所以凡三次方程式都是可用根式解的。
再看一般的四次方程式ax4+bx3+cx2+dx+e=0
它在一个含有其系数的数域中的群元素个数是 4!=24。这个群的组合因数是:
2,3,2,2。
这些都是质数,所以凡四次方程式也都可以用根式解。
对于一般的五次方程式,含有 5!个置换,其组合的因数是 2 与 5!/2 而 5!/2 不是质数,所以,一般的五次方程式不能用根式解。
如此,应用伽罗瓦群的理论,可以得到一个简单而有力的方法来决定一个方程式能否用根式解。
- 用直尺与圆规的作图
伽罗瓦在发明了判别方程式能否用根式解的鉴定之后,又创造了如何求一个能用根式解的方程式的根的方法,即利用一组“辅助方程式”,而这些辅助方程式的次数则是原方程式的群的组合因数。
其具体方法是:先把第一个辅助方程式的根加入数域 F 中,然后假设数域经第一个辅助方程式的根之加入而扩大了,并使分解因数的工作因之可以再继续下去,令方程式在这扩大了的数域 F1 中的群是 H。再将第二个辅助方程式的根加人 F1 中,使方程式的群变为 K,直到方程式在那个最后扩大成的数域 Fm 中的群是 1。而函数 x1 不能被 1 中的置换变更它的值,所以 x1 必在数域 Fm 中。同样,其余的根也都在 Fm 中。这样就可以得知什么样的数应加入原来的数域中,把方程式的群变为 1,从而决定方程式的根存在于怎样的数域中。以方程式 x3-3x+1=0
为例。此方程式在有理数域中的群由 1,( 1 2 3),( 1 3 2 )三
个置换作成。这个群的极大不变真约群是 1,组合因数是 3,所以只有一个辅助方程式,其次数是 3,这个辅助方程式的根含有一个立方根。所以这个立方根必须加入数域中,才能使方程式的群变为 1,而原来的方程式的根可从有理数域中的数及这个立方根单用有理运算得出。
只用直尺与圆规,能作直线和圆,这用代数表示是一次和二次方程式。所以,求它们的交点,只需解一个二次方程式就可以把交点的座标用有理运算和平方根表作系数的函数。因此,凡是能用直尺与圆规作出的数量都可以有限次的以加、减、乘、除和平方根表示。譬如有两线段 a,b 和单位长度, 可用直尺与圆规作出它们的和 a+b,差 a-b,积 ab,商 a/b 以及这
些量的平方根如
ab,
b等。
在讨论一个作图只用直尺、图规是否可能时,必须作出一个表示此种作图的代数学方程式。若此方程式在数域中能分解成单是一次和二次的代数式,则一切实数根都能用直尺与圆规作出。即使方程式不能分解成上述情况, 只要它的实数根能用有限次的有理运算与平方根表作已知的几何量的函数,
那么,作图只用直尺、圆规也是可能的。
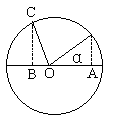
取 120°角来看假定此角位于一个半径是单位长的圆的中心,作出cos40°来,则只要取 OA=cos40°,于是 a 就是一个 40°的角,三等分 120
°的作图就完成了。利用三角恒等式: 2cos3a=8cos3a-6cosa,
令 x=2cosa,则上式化成2cos3a=x3-3x
因为 3a=120°, cos3a=-1/2;上式可写作 x3-3x+1=0 在半径是单位长的圆中,可作 OB=1/2,于是∠AOC=120°。
要解上面的方程式,必须把一个立方根加入于有理数域中。但一个立方根是不能用直尺与圆规作出的,因此可知:用直尺与圆规三等分任意角是不可能的。
用相似的方法,还可证明用直尺、圆规解决立方倍积问题也是不可能的。7.伽罗瓦的鉴定是正确的
在解方程式时,可利用方程式的根与系数之间的关系。例如在二次方程
式
x2+bx+c=0
的两个根 x1,x2 中,可得x1+x2=-b ①
与 x1x2=c ②
的关系。那么,能不能从这两个方程式中解 x1 与 x2 呢?不可以。因为如
果从①中得出 x1 的值而后代入②中,结果是x22+bx2+c=0,
这与原二次方程式丝毫没有分别。所以,这个方法行不通。但是,如果能得到一对都是一次的方程式,则 x1 和 x2 就可求了。
首先设方程式f(x)=0
有 n 个相异的根,而且在由方程式的系数及 1 之 n 个 n 次根决定的数域中,此方程式的群是一个元素个数为质数的巡回正置换群。其中,1 之 n 个 n 次根的含义是:
由 1 有三个立方根:
1, 1 1 1
− 2 + 2 − 3, − 2 −
en-1
可推出,在一般情况下,1 有 n 个 n 次根,记作:1,e,e2,⋯⋯,■
因为 1 个三个立方根只包含有理数和有理数的根数,所以 1 的 n 个 n 次
根也只包含有理数和有理数的根数。这种数加入数域中去,不影响方程能用
根式解。
举一将 n 个方程式写作一个的一组一次方程为例:x1+ρkx2+ρ2kx3
+⋯⋯+ρ(n-1)kxn=rk,③此处 k 的值可为 0 与 n-1 之间的任何整数,如当 k=0 时,③就为
x1+x2+x3+⋯⋯+xn=r0
当 k=1 时,③为x1+ρx2+ρ2x3+⋯⋯+ρn-1xn=r1, 以下,依次类推。
因为一个方程式的最高次项系数若是 1,则诸根之和等于方程式中第二
项的系数的负值,所以 ro 之值可以直接从方程式的系数中求得。如果把置换
(1 2 3⋯⋯n)用于③式的左端,③式左端为x2+ρkx3+ρ2kx4+⋯⋯+ρ(n-1)kx1
所以说置换(1 2 3⋯⋯n)
将 rk 之值变为ρ-krk。又因 Pn=1,故
(rk)n=(ρ-krk)n,
所以置换(1 2 3⋯⋯n)不变更 rnk 的值。同理,群中其它置换也不改变 rnk 的值。这就是说,所有 r 的值都可由根式得到。由③,可将 x 用ρ与 r 表示,则方程式③可用根式解。这样,就证明了:如果方程式在一个数域中的群是元素个数为质数巡回正置换群,则此方程式一定能用根式解。
举例来说,方程式
x3-3x+1=0
在有理数域中的群是 1,(1 2 3),(1 3 2)。它是一个元素个数为质数的巡回正置换群,所以可从 x1+x2+x3=0,
x1+ωx2+ω2x3=r1, x1+ω2x2+ωx3=r2,
这三个一次方程式中解它。此处ω表示 1 的一个虚立方根,r1 与 r2 可以
由数域中的数的根数得出。换句话说,如果把这种根数加入到数域中,则 x 都存在于扩大的数域中。
在一般情况下,常可以
y2=(x1-x2)2(x1-x3)2⋯⋯(xn-1-xn)2 作第一个辅助方程式,其右端是所有每两个根之差的平方之积。假如方程式的第一项系数是 1 的话,那么,上式右端则是方程式的“判别式”。例如二次方程式
x2+bx+c=0
的两个根 x1,x2 的差的平方是
(x1-x2)2=(x1+x2)2-4x1x2=b2-4c,这恰是方程式的判别式。同样, 高次方程式的判别式也可从系数求得。
再设所要解的方程式是一般的三次方程式,将第一个辅助方程式的根加
入原数域后,方程的群为 H,即一个元数为质数的巡回正置换群。这样,可利用
x1+x2+x3=-b,
x1+ωx2+ω2x3=r1,x1+ω2x2+ωx3=r2,
这三个一次方程式来解原三次方程式。其中 r1,r2 可由数域中数的根数求得。x1 ,x2,x3 存在于这个最后经 r1,r2 的加入而扩大成的数域中。
这样就证明了:方程式在一个由其系数与 1 之 n 个 n 次根而决定的数域中的群若是一个可解群,则此方程式是可以用根式解的。
伽罗瓦的群论,是解决数学问题的重要工具,它对于数学就如同语言对于人的重要性一样。正像人们评价的,“无论在什么地方,只要能应用群论, 就能从一切纷乱混淆中立刻结晶出简洁与和谐”。“群的概念是近世纪科学思想出色的新工具之一”。
